CONSTRUCCIONES

CONSTRUIR UN CUADRADO CONOCIENDO EL LADO ( Con regla y compás)
http://www.scribd.com/full/7970128?access_key=key-8gu8ou0fh1g5mkdqzj

CONSTRUIR UN RECTÁNGULO CONOCIENDO LOS LADOS ( con regla y compás)
http://www.scribd.com/full/7970130?access_key=key-68sn07b462jlh5ewfq2

CONSTRUIR UN ROMBO CONOCIENDO LA DIAGONAL Y EL LADO
http://www.scribd.com/full/7970132?access_key=key-1qtxmugtsojc2sm0yeuf

CONSTRUIR UN ROMBOIDE CONOCIENDO DOS LADOS Y UNA DIAGONAL.
http://www.scribd.com/full/7970131?access_key=key-25v2iqwij427v1otp8ny

GEOMETRÍA DEL ESPACIO

Para leer y observar simulaciones sobre geometría del espacio pueden visitar:
http://mimosa.pntic.mec.es/clobo/geoweb/espa1.htm

GEOMETRÍA DEL PLANO

En esta página encontrarán los conceptos primitivos de la geometría y todas las figuras del plano (Recuerden que el romboide en este material es llamado cometa ) 
  Interesante material para estudiar definiciones y propiedades de las figuras observando simuladores digitales que nos muestran relaciones, propiedades, representaciones, etc.
También está acompañado de ejercitación relativa a cada concepto.

http://mimosa.pntic.mec.es/clobo/geoweb/recta1.htm

CONSTRUCCIÓN DE UN HEXÁGONO REGULAR

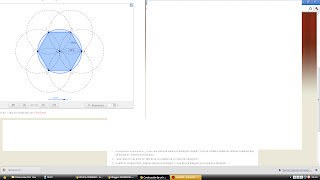Los polígonos regulares tienen la particularidad de ser figuras convexas con lados y ángulos congruentes. Dentro de estos polígonos el hexágono, figura del plano de seis lados, tiene la particularidad que al ser inscripto en una circunferencia, el radio de la misma es igual al lado del polígono. La siguiente animación les permitirá observar la construcción de un hexágono regular. Haz clic en reproduce.
http://www.proyectoscprgijon.es/mateprimaria/index.php?option=com_content&view=article&id=68:construccion-de-un-hexagono-regular&catid=19:otros-poligonos&Itemid=15

EL SISTEMA DE NUMERACIÓN MAYA

EL SIGUIENTE VÍDEO NOS PERMITIRÁ COMPRENDER FÁCILMENTE EL SISTEMA DE NUMERACIÓN MAYA QUE ES UN SISTEMA POSICIONAL DE BASE 20.
AUNQUE LOS MAYAS PARA EL TERCER NIVEL NO UTILIZARON 400 SINO 360 Y PARA EL CUARTO NIVEL 360X20 ES DECIR MULTIPLICABAN POR 7.200. EL VIDEO RESPETA LA BASE 20 EN FORMA ESTRICTA CUESTIÓN QUE LOS MAYAS NO TERMINARON DE INTERPRETAR.





OTRO VIDEO UBICÁNDONOS EN LA HISTORIA DE ESTA CIVILIZACIÓN QUE FUE LA PRIMERA EN UTILIZAR EL CERO

EL SISTEMA DE NUMERACIÓN DECIMAL

Nuestro sistema de numeración utiliza 10 símbolos para escribir todos los números, a dichos símbolos se los denomina cifras.
Los números de una sola cifra se denominan dígitos.
Nuestro sistema se rige por dos leyes: la ley de base y la ley de posicionalidad.  Es posicional porque la  cifra toma un valor relativo a la posición que ocupa. Es decir una de las grandes leyes que lo rige es la posicionalidad y la otra es la ley de base o de agrupamiento, en nuestro sistema se agrupa de a diez, diez unidades de un orden permiten formar una unidad del orden inmediato superior, es así como 10 unidades forman una decena, 10 decenas forman una centena, 10 centenas forman una unidad de mil, etc.
Cuando se forman una o más unidades del orden inmediato superior se escriben a la izquierda del número.
La siguiente aplicación permitirá comprender como armar el número agrupando elementos y recíprocamente como descomponer la cifra según su posición para determinar la cantidad de elementos que representa.

http://nlvm.usu.edu/es/nav/frames_asid_209_g_1_t_1.html?open=activities&from=category_g_1_t_1.html
(para la ejecución es necesario aceptar la ejecución). La misma aplicación permite ver la formación de números en otras bases diferente a la base 10 teniendo en cuenta los agrupamientos, canjes y posición respectiva.

Comprender cómo se escriben y cómo se leen los números implica comprender el valor relativo que tienen los números según la posición que ocupan, como así también poder establecer una relación entre el sistema de numeración oral y el sistema de numeración escrito.
Ejercicios de este tipo permiten tales descubrimientos:

Descomposicion de un numero segun el valor relativo de sus cifras

http://www.soloprofes.com/repositorio/mate_actividad1_1.swf

Composición del número conociendo el valor relativo de las cifras

Descomposición de un número y su lectura

Escritura de números

http://www2.gobiernodecanarias.org/educacion/17/WebC/eltanque/todo_mate/actividades5/tema1_P2/tema1_pr2.swf

Relaciones de orden

http://www2.gobiernodecanarias.org/educacion/17/WebC/eltanque/todo_mate/actividades5/tema1_P4/tema1_pr4_p.html

Aplicación completa de Anaya sbre el tema completa

http://www.ceipjuanherreraalcausa.es/Recursosdidacticos/TERCERO/datos/03_mates/U01/unidad01.htm

Página del gobierno de Canarias con la secuencia completa
http://www2.gobiernodecanarias.org/educacion/17/WebC/eltanque/todo_mate/actividades5/tema1_5_p.html

Muestra del libro digital de Digital-Text y Océano referente a los números naturales.

http://www.digital-text.com/muestra_capitulos/zz_Primaria/base.html?asi=pma&cur=5&uni=011&lan=es&modo=1

EL SISTEMA DE NUMERACIÓN ROMANO

El sistema de numeración romano es no posicional. Utiliza para representar todos los números siete.letras mayúsculas que son los símbolos del sistema. Cada una de ellas  riene un valor numérico absoluto.
I=1     V=5    X= 10   L=50     C=100  D =500       M=1.000
Todo sistema se rige por reglas para combinar los símbolos y poder escribir todos los números. Para conocer y aplicar esas reglas pueden trabajar con la ob aplicación del Gobierno de Canarias:

http://www2.gobiernodecanarias.org/educacion/17/WebC/eltanque/todo_mate/actividades5/tema1_P5/tema1_pr5.swf

Para para practicar conversiones del sistema de numeración decimal al romano y viceversa pueden acceder a un convertidor disponible en la página:

http://www.vivir.com/vivir/universidad/index.htm?http://www.vivir.com/vivir/universidad/convnumromanos.htm

Para practicar jugando ir a:
http://www.genmagic.org/mates3/nro1c.swf

http://www2.gobiernodecanarias.org/educacion/17/WebC/eltanque/todo_mate/actividades5/tema1_P6/tema1_pr6_p.html

Para cerrar el tema miremos un video por si quedaron dudas:

PATRONES Y REGULARIDADES

Según los autores A. Rabino, Ana Bressan y Fernanda Gallego: Un patrón es una sucesión de signos (orales, gestuales, gráficos, geométricos,numéricos, etc.) que se construye siguiendo una regla o algoritmo.
Desde situaciones muy sencillas los alumnos pueden aprender a identificar regularidades, reconocer un mismo patrón bajo diferentes formas y usar patrones para predecir valor.
Los siguientes videos nos informan sobre el tema:




Para practicar con patrones de  colores:
http://nlvm.usu.edu/es/nav/frames_asid_184_g_1_t_1.html?from=category_g_1_t_1.html

Para practicar con patrones numéricos:

http://nlvm.usu.edu/es/nav/frames_asid_185_g_1_t_1.html?from=category_g_1_t_1.html

VIDEO SOBRE LOS NÚMEROS

SE APRENDE JUGANDO

En el Nivel Inicial se aprende jugando y matemática se aprende resolviendo problemas. De lo que podremos deducir que los conceptos matemáticos aparecen  en  la sala como una necesidad para ganar el juego. 
Los juegos con dados, cartas, dominó, espaciales....con reglas para jugar y estrategias para ganar son verdaderos desafíos donde el contenido aparece como la mejor estrategia para lograr un resultado favorable.
Por eso vamos a jugar y enfrentar desafíos que nos lleven a buscar estrategias y nuevas formas de pensar ante situaciones problemáticas.Situaciones problemáticas  que nos lleven a actuar y reflexionar sobre las decisiones que vamos tomando.....suerte!!!

 "CÁNIVALES Y MISIONEROS"(juego gratuito de plastelina) http://www.plastelina.net/esp.htm.

HACIENDO  CLIC  EN LA PALABRA AQUÍ  O EN LA IMAGEN PODRÁS DESCARGAR EL JUEGO. ( BUSCAR EN DESCARGAS Y HACER DOBLE CLIC SOBRE EL ARCHIVO O  ACEPTANDO LA OPCIÓN EJECUTAR)  MAXIMICEN LA PANTALLA PARA VER MEJOR EL JUEGO Y ÉXITO...

 aquí

• OBJETIVO DEL JUEGO
• Tienen que lograr que queden los 3 caníbales y los tres misioneros en la otra orilla. 
• REGLAS DEL JUEGO SON LAS SIGUIENTES:
• En la barca sólo pueden ir dos tripulantes  (haciendo clic en el tripulante se sube a la barca, haciendo clic en GO se va a la otra orilla).
• Pero cuidado! porque cuando queden más caníbales que misioneros los cánibales se los comen.

Las Torres de Hanoi  ( haciendo clic en la imagen pueden acceder al juego) 
juego que se encuentra en la Biblioteca Nacional de Manipuladores Virtuales

El objetivo es:

Mover un grupo de discos de una estaca a otra usando el menor número de movidas posible.

 Las reglas:

• Puedes mover solamente un disco a la vez.
• No puedes colocar ningún disco sobre otro disco más pequeño.

Modo de Juego

• Para mover un disco arrastrarlo.
• Haciendo clic en deshacer puedes deshacer la última jugada.
• Puedes reiniciar el juego desde el botón reiniciar.
• Puedes elegir la cantidad de discos desde la parte inferior. Comienza jugando con tres discos y sigue avanzando, cada vez será más complejo. Mide tu ingenio.  
•  
• RANAS SALTARINAS

"Hacer saltar las ranas marrones  y amarillas de tal modo que las amarillas ocupen el lugar de las marrones  y viceversa".DESCARGA DEL JUEGO
Hacer clic en la palabra aquí , abrir con microsof exel, aceptar y comenzar a jugar.

aquí.

REGLAS DEL JUEGO:

• Se puede mover una rana a la piedra vecina que esté vacía.
• Se puede saltar una rana siempre y cuando haya una piedra disponible.
• Para mover una rana hay que hacer clic sobre ella.

BIENVENIDAS

La matemática como ciencia surge como una necesidad  del hombre por ello es un instrumento de socialización y un objeto cultural.
Hacer  matemática es resolver problemas. 
Ustedes son  futuras maestras jardineras que van a hacer matemática junto a sus alumnos en las salas proponiendo situaciones didácticas que permitan la construcción de los objetos de estudio matemáticos desde situaciones cotidianas, reales, provistas de significación para los niños.
BIENVENIDAS a este espacio complementario del  Espacio Curricular: "Desarrollo del Pensamiento Matemático"